• Fraktály jsou “přírodní jev nebo matematický soubor, který vykazuje opakující se vzor, který se zobrazuje v každém měřítku”. 1
• Fraktály se opakují do nekonečna.
• Základem fraktálů je zlatý řez a Fibonacciho posloupnost.
• Vizuálně představují fraktály nekonečný vzor, který lze nekonečně zvětšovat.
• Fraktály se vyznačují soběpodobností na všech úrovních. Tomu se také říká “rozšiřující se symetrie” nebo “vyvíjející se symetrie”.
• Zdá se, že jsou složité a nepravidelné, ale mají rozpoznatelnou statistickou soběpodobnost.
• Fraktály jsou holografické. Vycházejí z poměru fí, který vychází z pětiúhelníku, jenž vychází z kruhu. Fraktály lze pozorovat ve všech aspektech přírody.
• Fraktály vedly vědce k závěru, že věci, které se zdají být chaotické, jsou ve skutečnosti organizované. Ukázalo se, že velmi složité jevy mají skrytý řád.

Tři Typy Fraktálů:

• Přírodní fraktály
• Geometrické fraktály
• Algebraické fraktály

Přírodní Fraktály

Přírodní fraktály lze pozorovat v přírodě. Objevují se například v horách, skalách, oblázcích, písku, mracích, blesku, řekách, stromech, rostlinách, listech atd.

Jsou vidět ve větvení a zakořeňování stromů a ve způsobu, jakým se větví říční sítě.

Jsou také vidět v Lichtenbergově “blesku”, který vzniká rychlým vybíjením elektronů v lucitu.

Fraktální struktury se vyskytují také v lidském těle v: neuronech v mozku, nervovém systému, kardiovaskulárním systému, lymfatickém systému a větvení plic.

Spirály v Přírodě

Spirála je další běžný fraktál tvořený jednoduchým opakováním a kombinováním expanze a rotace k vytvoření jeho formy (Vesmír je tvořen Tlakem nebo-li Potenciálem(.

• Turbulentní pohyb tekutin – mýdlo, oceány, atmosféra…atd.

• Loděnky

• Rostlinná říše – kaktus agáve, květiny, ananas, kapradina… atd

• Hurikány

• Spirální galaxie

Větvící Vzory

• Všechny vzorce větvení zahrnují efektivní distribuci energie v té či oné formě.

• Tvoří nejjednodušší způsob, jak spojit každou část dané oblasti pomocí nejkratší celkové vzdálenosti (nebo nejméně práce).

• Každá větev určité velikosti je vždy přečíslena větvemi nejbližší menší dimenze.

Symetrie Li

• Li symetrie jsou v přírodě velmi časté. Souvisejí s fraktálními vzory větvení.
• Jsou to samoorganizující se systémy v přírodě způsobené interakcí mezi procesy a materiály.
• “Obklopují nás a prostupují světem přírody, ale teprve v 50. letech 20. století začaly být tyto záhadné formy symetrie chápány jako samoorganizující se systémy díky průkopnické práci Alana Turinga. Číňané je však studují již po tisíciletí a právě od nich dostaly své jméno.”5

Jsou k vidění u

• značení zvířat – zebry, žirafy, gepardi, hadi, aligátoři a krokodýli, žaby, ještěři, sépií, ryb, leoparda, ocelota, jaguára, vzorů mořských skořápek, rybích šupin, řezů kostí, svalových vláken…”.
• hmyzu – brouk goliáš, obal křídla kobylky, žilky křídel, pavučiny
• rostlin – mořská řasa Irish Moss a další mořské řasy, struktura cévních buněk, tkáňotvorné parenchymatické rostlinné buňky, žilky listů, lišejníky, žaberní vzory na houbách
• protahovací vzory
• kůra stromů
• krajinné vzory

• vzory mraků, vzor vysušené bahnité laguny v Senegalu, topografie sněhových čar, vzory odtoku vody a lávy, pobřeží
• žebrování písečných dun
• proudící voda přes písek, bahno nebo jíl – žebrování půdy
• vzory prasklin v hlíně, keramice, vyprahlé půdě, starých barvách a gelech

• ledová stopa na okenních tabulích

• vzory písku a bahna usazující se ve vodě
• konvekční válečky roztříštěné kapaliny
• shlukování částic na kapalném médiu
• Kerrův magnetooptický jev v tenkém řezu baryovým feritem
• Magnetické vzory v bludišti v leštěném krystalu křemíku a železa
• Magnetické doménové obrazce

• minerální vzory – achát, malachit, jaspis, zvětšený povrch diamantu, brachiální složky v hadcové hornině, žule a mramoru

Geometrické fraktály

Geometrické fraktály jsou “hrubý nebo fragmentovaný geometrický tvar, který lze rozdělit na části, z nichž každá je (alespoň přibližně) zmenšenou kopií celku. “6

Sierpinského trojúhelník

• Sierpinskiho trojúhelník vzniká opakovaným odstraňováním prostředního trojúhelníku z předchozí generace.
• Vnější trojúhelníky se v každém kroku opakují s násobkem 3:
• 1, 3, 9, 27, 81, 243, 729… atd.

Kochova křivka

• Kochova křivka se vytvoří opakovaným nahrazováním každého segmentu tvaru generátoru menší kopií téhož generátoru.
• Je podobná pobřežní čáře. Její délka se zvětšuje, čím blíže ji měříte.

Platónská Tělesa

Pět platónských těles jsou geometrické fraktály. Každé platónské těleso se například vejde samo do sebe i mimo sebe a dokonale do sebe zapadá. Tento postup může teoreticky pokračovat dovnitř a ven až do nekonečna.

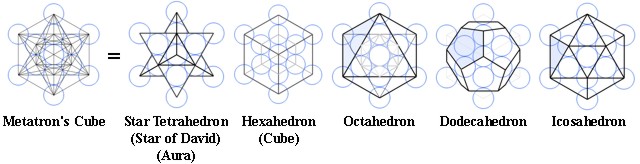
Platónská tělesa se také mohou různými způsoby vnořit do sebe jako množina. Jsou stvořena tak, aby mohla přecházet mezi tvary a zachovávat soběpodobnost ve všech měřítkách.

Algebraické fraktály

Mandelbrotova množin

Algebraické fraktály vznikají opakovaným výpočtem jednoduché rovnice. Známým příkladem je Mandelbrotova množina (the Mandelbrot Set).

Rovnice je následující:

Z_new= Z_old2 + C

Značka rovnosti je ve skutečnosti dvojitá šipka. Jedná se o rovnici nekonečné smyčky – systém neustálé zpětné vazby.

Benoit Mandelbrot (1924-2010) byl polsko-francouzsko-americký matematik, který vymyslel slovo “fraktál” a objevil Mandelbrotovu množinu. Mandelbrot pracoval 35 let ve společnosti IBM a často vyučoval na Harvardu. Byl najat společností AT&T, aby analyzoval vzory interferenčních signálů. Našel graf pro to, jak se zastavuje elektrický proud.

Zajímavé je, že platónská tělesa se nacházejí v 3D Mandelbrotově množině. Můžete si zahrát hru na spojování bodů s hrbolky na obrazci a získat platónská tělesa.

Juliova Množina

Dalším známým příkladem je Juliova množina (Julia Set).

Rovnice je následující::

Z = Z² + C

Exponent lze zvýšit na Z³, Z⁴, Z⁵ a tak dále. Stupeň symetrie vždy odpovídá stupni exponentu.

Mandelbulb

Mandelbulb je 3D projev Mandelbrotovy množiny, kterou objevili Daniel White a Paul Nylander v roce 2009. K objevu Mandelbulbu použili sférický souřadnicový systém a důmyslnou matematiku. O tom pojednávají a ilustrují to na svých webových stránkách http://mandelbulb.com/.

Vnořená platónská tělesa se fraktalizují a vytvářejí koule v koulích (vnořené koule), které tvoří 3D Mandelbulb.

To ukazuje, jak Mandelbrotova množina ve skutečnosti popisuje 3D sférickou strukturu. Platónská tělesa jako těsně zabalené koule jsou velkým tajemstvím fraktálu Mandelbrot/Mandelbulb.

Přiblížit si Mandelbrotovu množinu neboli Mandelbulb je jako letět vesmírem a vidět všechno fraktální větvení měsíců, planet, slunečních soustav, hvězd, galaxií, kup galaxií a prázdnot.

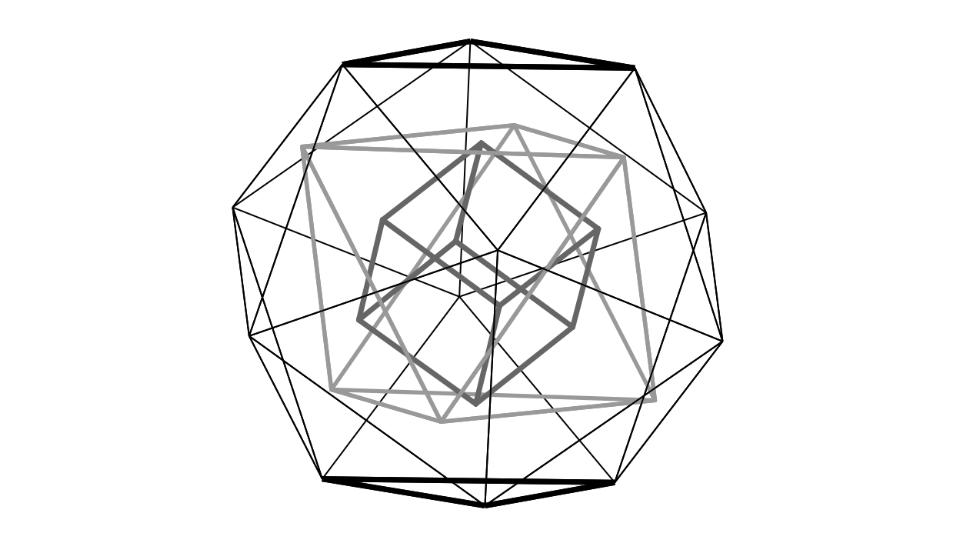
Platonic Solids as Spheres

Výše je uveden příklad rozpadu čtyřstěnu na hvězdicový čtyřstěn, poté na izotropní vektorovou matici a následně na další složitější verzi IVM. Pokud bychom tento tvar dále lámali směrem ven, nakonec by vytvořil dokonalou kouli.

Platónská tělesa jsou fraktální struktury a Platónská tělesa a Mandelbrotova množina spolu neoddělitelně souvisejí.

Phi – zlatý poměr – Φ

Zlatý poměr Phi je nesmírně důležitý pojem, který je třeba pochopit v matematice a geometrii.

• Botany – The Geometry of Plants – Part 10 – Fractals & Spirals
• The Holographic Universe – Part 1 – Fractals & Holography

Vlnová Genetika Léčí Downův Syndrom

Za použití technologie lingvistické vlnové genetiky bylo dosaženo pozitivních výsledků – Zvukový Vlnový Genetický Program od bratra Romana pomohl